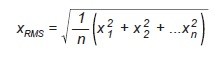Záleží na tom, jak definujete efektivní výkon.

Jak velký výkon se spotřebuje, když napětí sinusového průběhu 1Vef přiložíte k odporu 1 Ω?

To je zřejmé1 a není o tom sporu.
Teď se podívejme, jak lze výsledek srovnat s hodnotou z výpočtu efektivního výkonu.
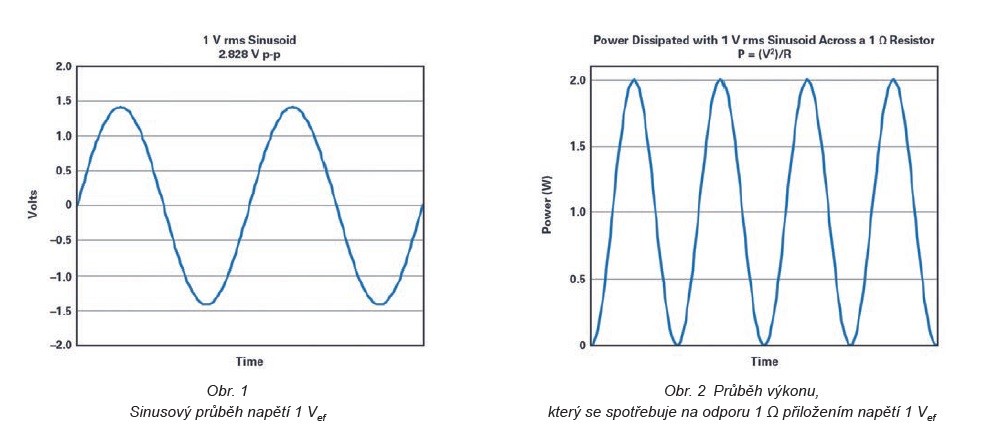
Obrázek 1 ukazuje sinusový průběh napětí s efektivní hodnotou 1 V.
Mezivrcholová hodnota = 1 Vef × 2 2 = 2,828 V, přičemž napěťový rozkmit je od +1,414 V do –1,414 V2.
Na obrázku 2 je vidět průběh výkonu, který se spotřebuje na odporu 1 Ω přiložením napětí 1 Vef (P = U2/R).
Jeden způsob, jak tuto hodnotu spočítat, je pomocí rovnice 23.
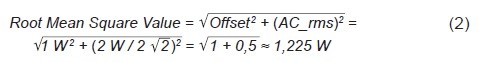
To lze ověřit použitím detailnějšího vzorce4 v prostředí MATLAB nebo v Excelu.
Výkon spotřebovaný na odporu 1 Ω přiložením sinusového napětí 1 Uef je 1 W, nikoli 1,225 W. Je to tedy střední hodnota výkonu, která odpovídá správné hodnotě, a je to tedy střední hodnota výkonu, která má fyzikální význam. Efektivní hodnota výkonu (tak jak je zde definována) nemá žádný zřejmý užitečný význam (žádný zřejmý fyzikální/elektrický význam) kromě toho, že se jedná o veličinu, kterou lze vypočítat jako cvičení.
Je velmi jednoduché provést tentýž rozbor s použitím sinusového proudu 1 Aef protékajícího odporem 1 Ω. Výsledek je stejný.
Napájecí zdroje pro integrované obvody jsou zpravidla stejnosměrné, takže pro IO efektivní výkon nehraje roli. Pro stejnosměrné parametry jsou střední a efektivní hodnoty vždy stejné jako stejnosměrné. Důležitost používání středního výkonu na rozdíl od výkonu efektivního, tak jak je definován v tomto článku, se týká výkonu napětí a proudů proměnných v čase, to znamená šumu, vf signálů a oscilátorů.
Používejte tedy efektivní hodnotu napětí a/nebo efektivní hodnotu proudu při výpočtu středního výkonu, a získáte tak jeho smysluplnou hodnotu.
Článek byl přeložen a poskytnut firmou Amtek s. r. o.
_________________________________________________________
1 Výkon spotřebovaný na odporu přiložením napětí je základní vztah, který lze snadno odvodit z Ohmova zákona (U = IR) a základních definic napětí (energie/náboj) a proudu (náboj/čas). Napětí × proud = energie/čas = výkon.
2 Rozkmit sinusoidy špička-špička je efektivní hodnota násobená 2 √2. Pro sinusové napětí Ušš = Uef × 2 √2, kde Ušš je napětí špička-špička a Uef je efektivní hodnota napětí. Toto je dobře známý vztah uvedený v bezpočtu učebnic, stejně jako na: en.wikipedia.org/wiki/root.mean.square.
3 Toto je převzato z efektivní hodnoty spočítané z konstantní hodnoty stejnosměrného posunu plus efektivní hodnoty střídavého průběhu zvlášť, stejně jako z aplikační poznámky „Make Better AC RMS Measurements with Your Digital Multimeter“ od Keysight.
4 Standardní učebnicová definice je jedním příkladem detailnějšího vzorce.