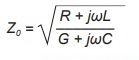Vítejte, dnes je
neděle
17.
listopad
2024
Odborný časopis a portál zaměřený na vývoj a výrobu elektroniky Každý rok se ve světě slaví svátek, jehož název i datum konání je odvozeno od matematické konstanty π. Tzv. Pi Day se koná 3. 14. (psáno v americkém formátu). Je zajímavé, že Albert Einstein se narodil 14. března, tedy právě na Pi Day, i když to bylo už v roce 1879.
Beru tento den vážně kvůli jeho významu v téměř každém oboru vědy, od astronomie, elektromagnetismu, fyziky až k několika dalším, o kterých se tu ani nerozepisuji. Jak si mohl výraz pí najít cestu do tolika vědeckých oborů a jaký je jeho dopad na elektromagnetismus?
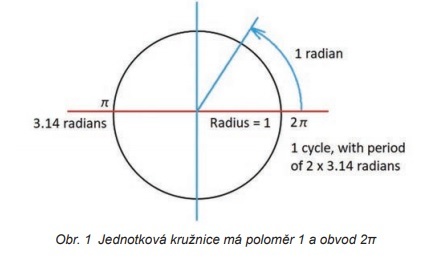
Ještě předtím, než zajdeme do detailů časové a frekvenční domény, bylo by vhodné připomenout si pojmy „jednotková kružnice“ a „radiány“. Jednotková kružnice je jednoduše kružnice s poloměrem 1, bez ohledu na jednotky. Obvod jednotkové kružnice je 2π, což znamená, že jeden cyklus bude 2π a na dokončení kružnice bude potřeba 2 × 3,14 radiánů, jak je vidět na obr. 1.
2π je perioda nebo obvod jednotkové kružnice. Bez matematického vztahu ke kružnici a k pí by bylo pro simulaci signálové integrity velmi obtížné modelovat chování signálů bez zhotovení desky plošných spojů a praktického měření na ní. Jinak řečeno, o tom, co by se mohlo stát, bychom se dozvěděli teprve tehdy, až by se to opravdu stalo.
Napojení úhlové frekvence na elektromagnetismus je probráno níže. V tuto chvíli stačí vědět, že počet oběhů kružnice za jednotku času je úhlová frekvence, která je dále typicky realizována v radiánech za sekundu.
Jsme přirozeně více znalí časové domény, se kterou se setkáváme v každodenním životě. Na druhé straně frekvenční doména může zajistit dobrý náhled do efektů signálové integrity, impedance a ztrát. Pro správné pochopení tohoto spojení je třeba si vysvětlit obě domény, časovou i frekvenční. Dr. Eric Bogatin ve své knize [1] vynikajícím způsobem vysvětluje jejich rozdíly i přednosti. S jeho svolením zde jeho informace použiji.
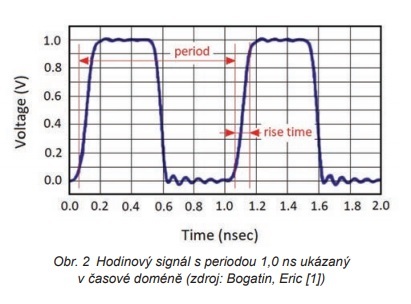
S použitím vztahů, které jsou dobře známé v časové doméně ukázané na obr. 2, reprezentuje Fclock počet cyklů za sekundu, což je obrácená hodnota periody hodin Tclock.
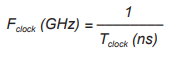
Výpočet je jednoduchý, když si dáme frekvenci v GHz a periodu hodin v ns. Signál na obr. 2 má frekvenci 1 GHz. Podobně by signál 10 GHz měl periodu 0,1 ns. Je důležité poznamenat, že časová doména je jedinou doménou, která je skutečná.
Jak je zmíněno výše, frekvenční doména zajišťuje hodnotný náhled na efekty signálové integrity, impedance a ztrát. Kdo se pohybuje kolem návrhu hardwaru delší dobu, jistě o frekvenční doméně slyšel. A právě zde se začíná objevovat pí.
Ve své knize [1] na ni Dr. Bogatin poukazuje takto: „Nejdůležitější kvalitou frekvenční domény je to, že není skutečná. Je to výtvor matematiky. Jedinou realitou je časová doména. Frekvenční doména je svět matematiky, kde se používají velmi specifická pravidla.“
Ve frekvenční doméně má všechno sinusový průběh a sinusovky jsou vším. Jakýkoliv tvar vlny v časové doméně může být kompletně charakterizován kombinací sinusových vln. Matematicky přitom víme o sinusovkách všechno.
Sinusové vlny zajišťují typicky přímější cestu k odpovědi na různé elektrické problémy, se kterými se často v signálové integritě setkáváme. Přenosové linky jsou ve zjednodušeném náhledu reprezentovány sítí rezistorů (R), indukčností (L) a kondenzátorů (C). Jak Eric ve své knize vyzdvihuje: „Když vyšleme signál jakéhokoliv průběhu, často dostaneme na druhém konci tvar vlny, který vypadá jako sinusová a může být jednoduše popsána kombinací několika sinusových vln.“
Při přechodu z časové do frekvenční domény není přidána žádná nová informace, a přesto se určité věci, včetně rozptylových parametrů (S-parametrů), ve frekvenční doméně objevují. Výsledky ze simulátoru signálové integrity mohou být zobrazeny buď ve frekvenční, nebo časové doméně. Názornou ilustraci jednoduchosti frekvenční domény ukazuje obr. 3.
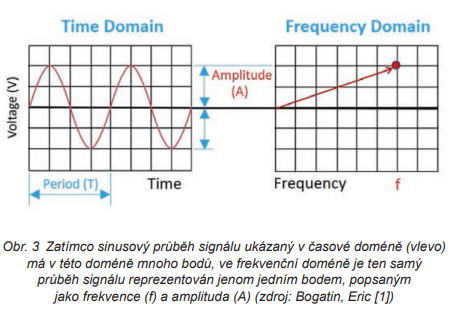
Tento obrázek je výstižnou ilustrací toho, jak je snadné popsat věci ve frekvenční doméně. Zatímco průběh signálu v časové doméně představuje stovky či tisíce bodů s daty, stejný průběh lze ve frekvenční doméně popsat frekvencí (f) a amplitudou (A).
Teď se ale můžete zeptat: „A co to má co dělat s pí?“. Tedy sinusové vlny mají amplitudu, frekvenci (a periody), stejně jako fázi. Frekvence (f, měřená v Hz) je počet kompletních cyklů sinusové vlny za sekundu. Úhlová frekvence je měřená v radiánech za sekundu. Jak je ukázáno na obr. 1, radiány popisují zlomek celého cyklu. V jednom kompletním cyklu je 2 × π radiánů. Jak mi můj přítel fyzik nedávno řekl: „My lidé si můžeme vymyslet úhlové systémy podle libosti, řekněme například 360°, protože takové číslo se pěkně dělí, ale je jen náhodně zvolené. Až se konečně potkáme s bytostmi s planety Zeta Reticuli, pravděpodobně zjistíme, že nemají kružnice s 360°, ale budou přitom souhlasit s tím, že kružnice nebo cyklus je 2π.“ Je to proto, že poměr mezi obvodem a poloměrem kružnice je stejný kdekoliv v prostoru.
Řecký znak omega (ω) je typicky používán pro úhlovou frekvenci měřenou v radiánech za sekundu. Frekvence sinusové vlny a úhlová frekvence mají mezi sebou následující vztah:
kde ω je úhlová frekvence v radiánech za sekundu a f je frekvence sinusové vlny v Hz. Když převedeme frekvenci na radiány za sekundu, matematický vztah komplexního systému se stane jednodušší, jak si ukážeme níže. Ale než necháme za sebou vztah mezi úhlovou frekvencí a frekvencí v časové doméně, ujistěme se, že jsme porozuměli jejich vzájemnému vztahu, protože ω ve frekvenční doméně převládá.
Jak už bylo zmíněno, přenosové linky mohou být reprezentovány sítí parazitních rezistancí (R), konduktancí (G), indukčností (L) a kapacitancí (C). Každá z nich stávajícímu toku proudu překáží. Tyto veličiny charakterizujeme takto:
– Rezistance (R) je impedance toku proudu reprezentovaného ideálním rezistorem v ohmech. Rezistance nemá žádný vztah k frekvenci.
– Reaktance (X) reprezentována v ohmech je impedance toku proudu z ideální indukčnosti (L) nebo kapacity (C). Reaktance závisí na frekvenci signálu.
– Impedance (Z) je reprezentována kombinací rezistance a reaktance, čímž je funkcí frekvence.
kde R a G (konduktance) reprezentují „skutečnou“ část impedance, zatímco jωL a jωC reprezentují „imaginární“ část impedance − induktivní a kapacitní reaktanci ve frekvenční doméně. Aniž bychom šli do detailů výrazu „imaginární matematika“, hodnota „j“ je druhou odmocninou z hodnoty –1. Protože taková druhá odmocnina neexistuje, používá se pojem „imaginární“.
Mohli bychom pokračovat dále a probrat také ztrátu vodiče a dielektrickou ztrátu ve frekvenční doméně. Opět se tu objeví úhlová frekvence, pí a imaginární matematika, ale to už by bylo dlouhé.
Nezbývá, než každému popřát Happy Pi Day!
[1] Bogatin, Eric. „Signal and Power Integrity – Simplified“
[3] Brooks, Douglas, „Signal Integrity Issues and Printed Circuit Board Design“
